Question

Imagine that you would like to purchase a $275,000 home. Using 20% as

a down payment (or $55,000), determine the monthly mortgage payment
for your dream home using the loan terms below. Hint: Read the Loan
Calculator tip at right for a tool that will help you make the calculations.
A. 15-year mortgage term with a 3% interest rate
Total Amount Paid Over Loan Term
Minimum Monthly Payment:
B. 20-year mortgage term with a 6% interest rate
Total Amount Paid Over Loan Term:
Minimum Monthly Payment:
C. 30-year mortgage term with a 5% interest rate
Total Amount Paid Over Loan Term:
Minimum Monthly Payment:
Which mortgage would you choose and why?

Answer 1

The mortgage chosen is option A;

15-year mortgage term with a 3% interest rate because it has the lowest total amount paid over the loan term of $270,470

Explanation:

The details of the home purchase are;

The price of the home = $275,000

The mode of purchase of the home = Mortgage

The percentage of the loan amount payed as down payment = 20%

The amount used as down payment for the loan = $55,000

The principal of the mortgage borrowed, P = The price of the house - The down payment

∴ P = $275,000 - 20/100 × $275,000 = $275,000 - $55,000 = $220,000

The principal of the mortgage, P = $220,000

The formula for the total amount paid which is the cost of the loan is given as follows;

`Outstanding \ Loan \ Balance = (P \cdot \left[\left(1+(r)/(12) \right)^n - \left(1+(r)/(12) \right)^m \right] )/(1 - \left(1+(r)/(12) \right)^n )`

The formula for monthly payment on a mortgage, 'M', is given as follows;

`M = (P \cdot \left((r)/(12) \right) \cdot \left(1+(r)/(12) \right)^n )/(\left(1+(r)/(12) \right)^n - 1)`

A. When the mortgage term, t = 15-years,

The interest rate, r = 3%

The number of months over which the loan is payed, n = 12·t

∴ n = 12 months/year × 15 years = 180 months

n = 180 months

The monthly payment, 'M', is given as follows;

M =

The total amount paid over the loan term = Cost of the mortgage

Therefore, we have;

220,000*0.05/12*((1 + 0.05/12)^360/( (1 + 0.05/12)^(360) - 1)

`M = (220,000 \cdot \left((0.03)/(12) \right) \cdot \left(1+(0.03)/(12) \right)^(180) )/(\left(1+(0.03)/(12) \right)^(180) - 1) \approx 1,519.28`

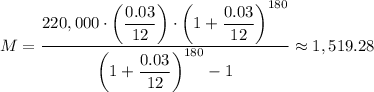
The minimum monthly payment for the loan, M ≈ $1,519.28

The total amount paid over loan term, A = n × M

∴ A ≈ 180 × $1,519.28 = $273,470

The total amount paid over loan term, A ≈ $270,470

B. When t = 20 year and r = 6%, we have;

n = 12 × 20 = 240

`\therefore M = (220,000 \cdot \left((0.06)/(12) \right) \cdot \left(1+(0.06)/(12) \right)^(240) )/(\left(1+(0.06)/(12) \right)^(240) - 1) \approx 1,576.15`

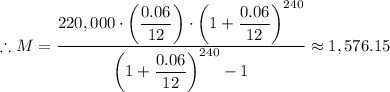
The total amount paid over loan term, A = 240 × $1,576.15 ≈ $378.276

The monthly payment, M = $1,576.15

C. When t = 30 year and r = 5%, we have;

n = 12 × 30 = 360

`\therefore M = (220,000 \cdot \left((0.05)/(12) \right) \cdot \left(1+(0.05)/(12) \right)^(360) )/(\left(1+(0.05)/(12) \right)^(360) - 1) \approx 1,181.01`

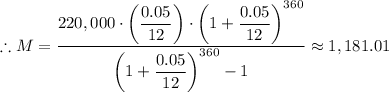
The total amount paid over loan term, A = 360 × $1,181.01 ≈ $425,163

The monthly payment, M ≈ $1,181.01

The mortgage to be chosen is the mortgage with the least total amount paid over the loan term so as to reduce the liability

Therefore;

The mortgage chosen is option A which is a 15-year mortgage term with a 3% interest rate;

The total amount paid over the loan term = $270,470