Question

Brook makes this conjecture: Because the angles are equal, the proportion of area of each sector relative to the area of the given circle is also equal.

Answer 1

The Brooks conjecture is true as the proportion of the area of a sector to the area of a circle is only dependent on the angle.

Explanation:

The area of a sector for a radius r and an angle θ is given as

`\Delta Sector=(1)/(2)r^2\theta`

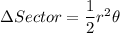
Whereas the area of a circle for a radius r is given as

`\Delta Circle=\pi r^2`

Now the ratio is given as

`(\Delta Sector)/(\Delta Circle)=((1)/(2)r^2\theta)/(\pi r^2)`

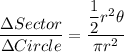
Here as r is the radius of the circle and it is the same therefore the above ratio is simplified to

`(\Delta Sector)/(\Delta Circle)=(\theta)/(2\pi )`

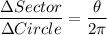
Here as π is constant the only variable here is θ. Thus according to Brooks conjecture when the angles are equal, the proportion of area of each sector relative to the area of the given circle is also equal is true.