Question

Test Booklet AP CollegeBoard AP Statistics Name Unit 7, part 2 Test (MC) 1. A statistics student wants to compare the mean times needed to access flight information for two major airlines. Twenty randomly selected students accessed one airline's Web site, and the time required to locate the flight information using the Web site had a mean of 2.5 minutes and a standard deviation of 0.8 minute. Twenty different randomly selected students accessed the other airline's Web site, and the time required to locate the flight information using the Web site had a mean of 2.1 minutes and a standard deviation of 1.1 minutes. Assuming that the conditions for inference are met, which of the following statements about the p- value obtained from the data and the conclusion of the significance test is true?

A. The p-value is less than 0.01; therefore, there is a significant difference in mean search times on the two Web sites
B. The p-value is greater than 0.01 but less than 0.05, therefore, there is a significant difference in mean search times on the two Web sites.
C. The p-value is greater than 0.05 but less than 0.10, therefore, there is a significant difference in mean search times on the two Web sites.
D. The p-value is greater than 0.10, therefore, there is no significant difference in mean search times on the two Web sites
E. Since this is a matched-pairs situation, additional information is needed to perform a test of significance

Answer 1

The statement about the p-value obtained from the data and the conclusion of the significant test that is true is option D

D. The p-value is greater than 0.10, therefore, there is no significant difference in mean search times on the two Web sites

Explanation:

From the question, the statistics student wants to compare the mean times needed to access flight information for two airlines

Let 'A' represent one of the airlines and let 'B' represent the other airline

In the statistics hypothesis test we have;

The mean time to access airline A's website,
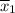`\overline x_1` = 2.5 minutes

The standard deviation to access airline A's website, s₁ = 0.8 minutes

The mean time to access airline B's website,
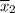`\overline x_2` = 2.1 minutes

The standard deviation to access airline B's website, s₂ = 1.1 minutes

The t-test is given as follows;

The null hypothesis is H₀; μ₂ - μ₁ = 0

The alternative hypothesis is H₀; μ₂ - μ₁ ≠ 0

`t=\frac{(\bar{x}_(1)-\bar{x}_(2))}{\sqrt{(s_(1)^(2) )/(n_(1))+(s _(2)^(2))/(n_(2))}}`

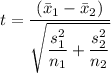
The critical-t at n₁ + n₂ - 2 = 20 + 20 - 2 = 38 degrees of freedom is therefore, from a graphing calculator, the critical-t = ±2.734 and the probability = 0.197;

`t=\frac{(2.5-2.1)}{\sqrt{(0.8^(2) )/(20)+(1.1^(2))/(20)}} \approx 1.32`

Therefore, given that the test statistic is smaller than the critical-t, and the p-value is greater than the significance level of 0.01 and is also larger than 0.10, therefore, there is no significant difference in mean search times on the two Web sites.