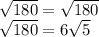Question

Need help pls and thank you​

Answer 1

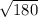`√(180)` and
`6√(5)`

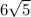
Explanation:

The easiest way to solve this problem is to look at all the simplified radicals on the right. Then un-simplify them by bringing the coefficients under the radical. If the radican (value under the radical) of the radical on the right is equal to the radican on the left, then the two radicals are equal.

To un-simplify a radical, one will square the coefficients and then multiply that value by the current radican of expression. The result is the un-simplified value of the radical.

A.

`3√(15)\\\\= √(15*(3)^2)\\\\=√(15*9)\\\\=√(135)`

`√(45) \\eq √(135)\\√(45) \\eq 3√(15)`

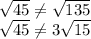
B.

`3√(5)\\\\=√(5*(3)^2)\\\\=√(5*9)\\\\=√(45)`

`√(75) \\eq √(45)\\√(75) \\eq 3√(5)`

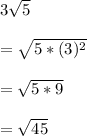
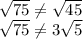
C.

`9√(6)\\\\=√(6*(9)^2)\\\\=√(6*81)\\\\=√(486)`

`√(54) \\eq √(486)\\√(54) \\eq 9√(6)`

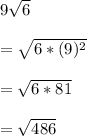
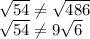
D.

`6√(5)\\\\=√(5*(6)^2)\\\\=√(5*36)\\\\=√(180)`

`√(180)=√(180)\\√(180)=6√(5)`