Question

A cylindrical cup is 8 centimeters in height. When filled to the very top, it holds 480 cubic centimeters of water. What is the radius of the cup, rounded to the nearest tenth? Explain or show your reasoning.

Answer 1

The radius of the cylindrical cup is approximately 7.7 centimeters.

Step-by-step explanation:

To find the radius of the cylindrical cup, we can use the formula for the volume of a cylinder: V = πr²h

Given that the cup holds 480 cubic centimeters of water and has a height of 8 centimeters, we can substitute these values into the formula:

480 = πr²(8)

Dividing both sides of the equation by 8π gives us:

r² = 60

Taking the square root of both sides of the equation, we find:

r ≈ 7.7 cm

Therefore, the radius of the cup is approximately 7.7 centimeters.

Answer 2

4.4cm

Step-by-step explanation:

The area of a circle is
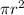`\pi r^(2)`, where r is the radius.

Hence the volume of the cylinder would be
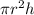`\pi r^(2)h`, where r is the radius and h is the height of the cylinder.

We can set up an equation V =
`\pi r^(2)h`

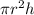
If we plug in the values we know, V=480, h=8, then we get
`480=8\pi r^(2)`

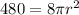
If we divide both sides be 8pi and square root both sides after that, we can find the value of r.

`r = \sqrt{(480)/(8\pi ) } =4.37019`

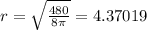
To the nearest tenth, the radius would round up, yielding 4.4cm