Question

On a coordinate plane, parallelogram R S T U has points (negative 4, 4), (2, 6), (6, 2), and (0, 0). What is the area of parallelogram RSTU? 24 square units 26 square units 32 square units 38 square units

Answer 1

Im pretty sure its 32

Explanation:

Answer 2

The area of the parallelogram is;

32 square units

Explanation:

The given parameters are;

The coordinates of the parallelogram RSTU = R(-4, 4), S(2, 6), T(6, 2), and U(0, 0)

We note that the area of a parallelogram = Base length × Height

From the drawing of the parallelogram RSTU, we have;

The base length = The length of
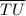`\overline {TU}` = The length of
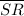`\overline {SR}` = √((2 - (-4))² + (6 - 4)²) = 2·√10

The height of a parallelogram is perpendicular to its base length = The line
`\overline {VT}`

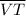
∴ Where, the slope of the base length = m, the slope of the height = -1/m

The slope, 'm' of
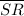`\overline {SR}` = (6 - 4)/(2 - (-4)) = 1/3

Therefore, the slope of the height = -1/(1/3) = -3

We note that a point on the height is the point 'T', therefore, the equation of the line in point and slope form is therefore;

y - 0 = -3·(x - 0)

∴ y = -3·x

Therefore, the coordinates of the point 'V' is given by the simultaneous solution of the equations of
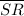`\overline {SR}` and
`\overline {VT}`

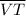
The equation of the line
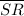`\overline {SR}` in point and slope form from the point 'R' and the slope 'm = 1/3' is given as follows;

y - 4 = (1/3) × (x - (-4)) = (1/3) × (x + 4)

y = x/3 + 4/3 + 4 = x/3 + 16/3

y = x/3 + 16/3

We then have the coordinate at the point 'V' (x, y) is given as follows;

-3·x = x/3 + 16/3

-9·x = x + 16

-10·x = 16

x = -16/10 = -1.6

x = -1.6

∴ y = -3·x = -3 × -1.6 = -4.8

y = 4.8

The coordinate at the point, V = (-1.6, 4.8)

The length of the line
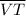`\overline {VT}` = The height of the parallelogram = √((-1.6 - 0)² + (4.8 - 0)²) = 8/5·√10

The height of the parallelogram = 8/5·√10

The area of the parallelogram, A = Base length × Height

∴ A = 2·√(10) × 8/5·√(10) = (16/5) × 10 = 32

The area of the parallelogram, A = 32 square units.