Question

A researcher is interested in finding a 95% confidence interval for the mean number minutes students are concentrating on their professor during a one hour statistics lecture. The study included 150 students who averaged 42 minutes concentrating on their professor during the hour lecture. The standard deviation was 12 minutes.

Round your answers to two decimal places.
A. The sampling distribution follows a ____ distribution.
B. With 95% confidence the population mean minutes of concentration is between_____ and_____ minutes.
C. If many groups of 150 randomly selected students are studied, then a different confidence interval would be produced from each group. About ______ percent of these confidence intervals will contain the true population mean number of minutes of concentration and about ______ percent will not contain the true population mean number of minutes of concentration.

Answer 1

A. Normal

B. Between 40.08 minutes and 43.92 minutes.

C. About 95 percent of these confidence intervals will contain the true population mean number of minutes of concentration and about 5 percent will not contain the true population mean number of minutes of concentration.

Explanation:

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

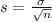For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
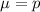`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

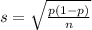
x% confidence interval:

A confidence interval is built from a sample, has bounds a and b, and has a confidence level of x%. It means that we are x% confident that the population mean is between a and b.

Question A:

By the Central Limit Theorem, a normal distribution.

Question B:

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1 - 0.95)/(2) = 0.025`

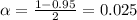
Now, we have to find z in the Ztable as such z has a pvalue of
`1 - \alpha`.

That is z with a pvalue of
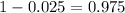`1 - 0.025 = 0.975`, so Z = 1.96.

Now, find the margin of error M as such

`M = z(\sigma)/(√(n))`

In which
`\sigma` is the standard deviation of the population and n is the size of the sample.

`M = 1.96(12)/(√(150)) = 1.92`

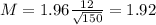
The lower end of the interval is the sample mean subtracted by M. So it is 42 - 1.92 = 40.08 minutes

The upper end of the interval is the sample mean added to M. So it is 42 + 1.92 = 43.92 minutes

Between 40.08 minutes and 43.92 minutes.

Question C:

x% confidence interval -> x% will contain the true population mean, (100-x)% wont.

So, 95% confidence interval:

About 95 percent of these confidence intervals will contain the true population mean number of minutes of concentration and about 5 percent will not contain the true population mean number of minutes of concentration.