Question

Sam kicks a ball from the ground with a starting velocity of 32 feet per second. The ball soars into the air, arcs down with parabolic motion, and lands back on the ground. Write an equation to describe the height of the ball as a function of time, using h(t)=-16t^2+vt+s. PLS HELP!!!!!!

Answer 1

The function that describes the height of the ball in time is
`h(t) = 32\cdot t -16.087\cdot t^(2)`.

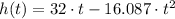Explanation:

Let suppose that ball experiments a free fall motion, which means that the ball is accelerated because of gravity and gravitational acceleration can be considered constant since height reached by the object is too small in comparison with the radius of the Earth. Therefore, we can assume that ball is accelerated uniformly.

Hence, the kinematic formula for the height of the ball (
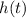`h(t)`), in feet, is described below:

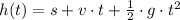`h(t) = s + v\cdot t + (1)/(2)\cdot g \cdot t^(2)` (1)

Where:

`s` - Initial height with respect to the ground, in feet.

`v` - Initial velocity, in feet per second.

`t` - Time, in seconds.

`g` - Gravitational acceleration, in feet per square second.

If we know that
`s = 0\,ft`,
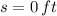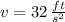`v = 32\,(ft)/(s^(2))` and
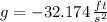`g = -32.174\,(ft)/(s^(2))`, then the function that describes the height of the ball in time is:

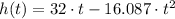`h(t) = 32\cdot t -16.087\cdot t^(2)` (2)