Question

A magician claims that he/she has invented a novel, super-fantastic heat engine. This engine operates between two reservoirs of temperatures 250 K and 750 K, respectively. Please verify and explain if this is possible for any of the following QH (heat received from the hot reservoir), QL (heat rejected to the cool reservoir), and W (mechanical work produced):

a. (3a). (3p) QH= 900 kJ, Wmech = 400 kJ, QL = 600 kJ.
b. (3b). (3p) Qu= 900 kJ, W mech = 400 kJ, QL = 500 kJ.
c. (3c). (3p) Qh= 900 kJ, Wmech = 600 kJ, QL = 300 kJ.
d. (3b). (3p) Qh= 900 kJ, Wmech = 800 kJ, QL = 100 kJ.

Answer 1

A) Not possible, B) Posible, C) Possible, D) Not possible.

Step-by-step explanation:

The maximum theoretical efficiency for any thermal engine is defined by Carnot's cycle, whose energy efficiency (
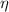`\eta`), no unit, is expressed below:

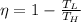`\eta = 1-(T_(L))/(T_(H))` (1)

Where:

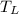`T_(L)` - Cold reservoir temperature, in Kelvin.

`T_(H)` - Hot reservoir temperature, in Kelvin.

If we know that
`T_(L) = 250\,K` and
`T_(H) = 750\,K`, then the maximum theoretical efficiency for the thermal engine is:

`\eta = 1-(T_(L))/(T_(H))`

`\eta = 0.667`

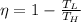
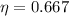
For real thermal engines, the following inequation is observed:

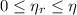`0 \le \eta_(r) \le \eta` (2)

Where
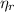`\eta_(r)` is the efficiency of the real heat engine, no unit.

There are two possible criteria to determine if a given heat engine is real:

Efficiency

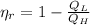`\eta_(r) = 1 - (Q_(L))/(Q_(H))` (3)

Where:

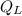`Q_(L)` - Heat rejected to the cold reservoir, in kilojoules.

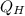`Q_(H)` - Heat received from the hot reservoir, in kilojoules.

Power output

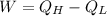`W = Q_(H)-Q_(L)` (4)

Where
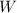`W` is the power output, in kilojoules.

Now we proceed to verify each case:

A)
`Q_(H) = 900\,kJ`,
`Q_(L) = 600\,kJ`,
`W_(m) = 400\,kJ`

`\eta_(r) = 0.333`

`0 \le \eta_(r) \le \eta`

`W = 300\,kJ`

`W \\e W_(m)`

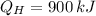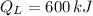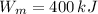
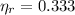
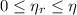
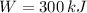
This engine is not possible.

B)
`Q_(H) = 900\,kJ`,
`Q_(L) = 500\,kJ`,
`W_(m) = 400\,kJ`

`\eta_(r) = 0.444`

`0 \le \eta_(r) \le \eta`

`W = 400\,kJ`

`W = W_(m)`

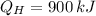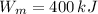
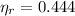
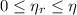
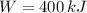
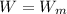
The engine is possible.

C)
`Q_(H) = 900\,kJ`,
`Q_(L) = 300\,kJ`,
`W_(m) = 600\,kJ`

`\eta_(r) = 0.667`

`0 \le \eta_(r) \le \eta`

`W = 600\,kJ`

`W = W_(m)`

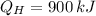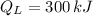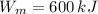
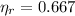
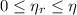
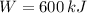
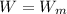
The engine is possible.

D)
`Q_(H) = 900\,kJ`,
`Q_(L) = 100\,kJ`,
`W_(m) = 800\,kJ`

`\eta_(r) = 0.889`

`\eta_(r) > \eta`

`W = 800\,kJ`

`W = W_(m)`

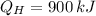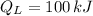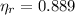
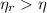
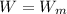
The engine is possible.