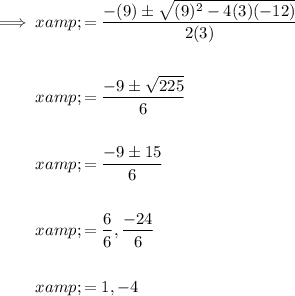Answer:

Explanation:
Quadratic Formula
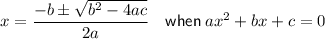
A linear equation in the form
 cannot be solved using the quadratic formula, as it is not a quadratic equation.
cannot be solved using the quadratic formula, as it is not a quadratic equation.
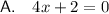
This is a linear equation and therefore cannot be solved using the quadratic formula.
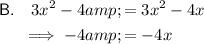
This is a linear equation and therefore cannot be solved using the quadratic formula.
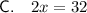
This is a linear equation and therefore cannot be solved using the quadratic formula.

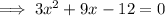
Therefore, this is a quadratic equation in the form
 and therefore can be solved quadratic formula.
and therefore can be solved quadratic formula.
a = 3, b = 9 and c = -12
Inputting these into the quadratic formula and solving for x: