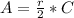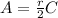Question

Describe the relationship between the area of a circle and its circumstances

Answer 1

`A = (r)/(2)C`

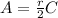
Explanation:

Given

Shape: Circle

Required

The area and the circumference (relationship)

This implies that, we write an expression that relates the area and the circumference.

Circumference is calculated as:

`C = 2\pi r`

Area is calculated as:

`A = \pi r^2`

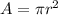
The area can be rewritten as:

`A = (2\pi r^2)/(2)`

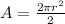
Further rewrite as:

`A = (r)/(2)*2\pi r`

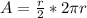
Recall that:
`C = 2\pi r`

So, the expression becomes

`A = (r)/(2)*C`

`A = (r)/(2)C`