Answer:
The pvalue of the test is 0.0784 > 0.01, which means that at this significance level, we do not reject the null hypothesis that the percentage of blue candies is equal to 29%.
Explanation:
The candy company claims that the percentage of blue candies is equal to 29%.
This means that the null hypothesis is:
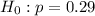
We want to test the hypothesis that this is true, so the alternate hypothesis is:
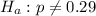
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
0.29 is tested at the null hypothesis:
This means that
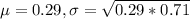
Suppose that in a random selection of 100 colored candies, 21% of them are blue.
This means that

Value of the test statistic:

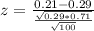
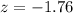
Pvalue of the test:
The pvalue of the test is the probability of the sample proportion differing at least 0.21 - 0.29 = 0.08 from the population proportion, which is 2 multiplied by the pvalue of Z = -1.76.
Looking at the z-table, z = -1.76 has a pvalue of 0.0392
2*0.0392 = 0.0784
The pvalue of the test is 0.0784 > 0.01, which means that at this significance level, we do not reject the null hypothesis that the percentage of blue candies is equal to 29%.