Question

Please help me with this math problem.

Answer 1

The table is a quadratic function

Explanation:

Given

The attached table

Required

Tell if it is a quadratic function

The difference in the x values are uniform (i.e. difference of 1), so the following method can be applied.

(1) Subtract adjacent y values.

`d_1=2 - 16 = -14`

`d_2=-2 - 2 = -4`

`d_3 = 4--2 = 6`

`d_4 = 20 - 4 = 16`

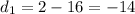
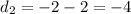
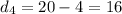
(2) Subtract adjacent differences in (1) above

`d_5 = d_2 - d_1 = -4 --14 = 10`

`d_6 = d_3 - d_2 = 6 --4 = 10`

`d_7 = d_4 - d_3 = 16 -6 = 10`

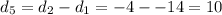
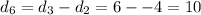
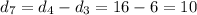
Notice the calculated differences in (2) are the same.

Hence, the table is a quadratic function