Question

Which transformations are needed to change the parent cosine function to y = 3 cosine (10 (x minus pi))?

Answer 1

See Explanation

Explanation:

Given

New function:
`y = 3 \cos(10 (x -\pi))`

We can assume the parent function to be:

`y = \cos (x)`

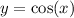
The new function can be represented as:

`y = A*\cos(((2\pi)/(B))(x-c))`

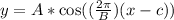
Where

A = Vertical stretch factor

B = Period

C = Right shift

By comparison:

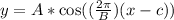`y = A*\cos(((2\pi)/(B))(x-c))` to
`y = 3 \cos(10 (x -\pi))`

`A = 3`

`c = \pi`

`(2\pi)/(B) = 10`

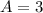
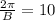
Solve for B

`B = (2\pi)/(10)`

`B = (\pi)/(5)`

Using the calculated values of
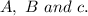`A,\ B\ and\ c.` This implies that, the following transformations occur on the parent function:

• Vertically stretched by
  `3`
• Horizontally compressed by
  `(\pi)/(5)`
• Right shifted by
  `\pi`