Answer:
ratio's of their volume is 216 : 343
Step-by-step explanation:
Let volume of one solid be x, another be y
given scale factor = 6 : 7
volume of solid = a³
solve:
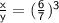
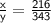
║ Therefore volume of one solid is 216 and another 343 ║
In ratio form:
216 : 343