Answer:

Explanation:
This triangle has a small square, which represents a right angle. Therefore, we can use the Pythagorean Theorem.

Where a and b are the legs of the triangle and c is the hypotenuse.
In this triangle, 7 and √15 are the legs, because these sides make up the right angle. The unknown side is the hypotenuse, because it is opposite the right angle. So, we know two values:
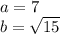
Substitute these values into the formula.
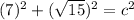
Solve the exponents.

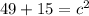
Add.
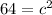
Since we are solving for c, we must isolate the variable. It is being squared and the inverse of a square is the square root. Take the square root of both sides.
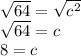
The third side length is 8.