Question

4. If 52.0 g of magnesium react with excess hydrochloric acid, how many liters of hydrogen gas can be made at 300 K and 0.970 atm?

Answer 1

Answer: 54.8 Liters of hydrogen gas can be made at 300 K and 0.970 atm

Step-by-step explanation:

To calculate the moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text {Molar mass}}`

`\text {moles of magnesium }=(52.0g)/(24g/mol)=2.16moles`

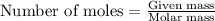
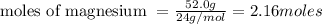
The balanced chemical equation is:

`Mg+2HCl\rightarrow MgCl_2+H_2`

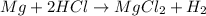
According to stoichiometry:

1 mole of Mg gives = 1 mole of
`H_2`

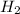
Thus 2.16 moles of Mg give =
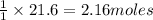`(1)/(1)* 21.6=2.16 moles` of
`H_2`

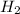
According to ideal gas equation:

`PV=nRT`

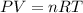
P = pressure of gas = 0.970 atm

V = Volume of gas = ?

n = number of moles = 2.16

R = gas constant =
`0.0821Latm/Kmol`

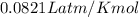
T =temperature =
`300K`

`V=(nRT)/(P)`

`V=(2.16mol* 0.0821Latm/Kmol* 300K)/(0.970atm)=54.8L`

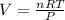
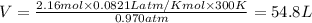
Thus 54.8 Liters of hydrogen gas can be made at 300 K and 0.970 atm