Answer:
(a)


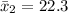
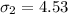
(b)

(c)
 to
to
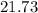
Explanation:
Given

And the accompanying data for private (1) and public (2) colleges
Solving (a): The sample mean and sample standard deviations
Private College
Calculating sample mean
This is calculated as:
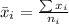
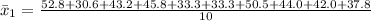


Calculating sample standard deviation
This is calculated as:
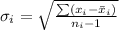
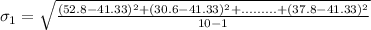
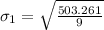
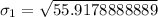
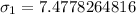
 -- approximated
-- approximated
Public College
Calculating sample mean
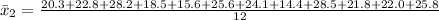
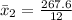
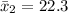
Calculating sample standard deviation
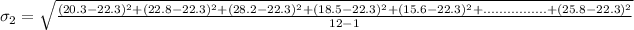

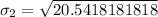
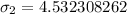
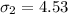 -- approximated
-- approximated
Solving (b): Point estimate of the difference between the two population means
This is calculated as:

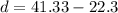

Solving (c): 95% confidence interval
First, calculate the degrees of freedom:
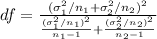
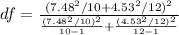

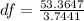
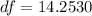
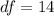
Calculate the critical value (t)
At 95% confidence interval and df = 14;
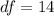
The confidence interval is then calculated as:

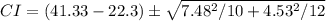
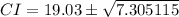
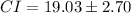
Split
 to
to
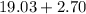
 to
to
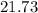
This implies that:
Private colleges have population mean annual cost of $16.33 to $21.73 more expensive than public colleges