Question

Canadians who visit the United States often buy liquor and cigarettes, which are much cheaper in the United States. However, there are limitations. Canadians visiting in the United States for more than

asked Jun 1, 2022 36.8k views

Canadians who visit the United States often buy liquor and cigarettes, which are much cheaper in the United States. However, there are limitations. Canadians visiting in the United States for more than 2 days are allowed to bring into Canada one bottle of liquor and one carton of cigarettes. A Canada Customs agent has produced the following joint probability distribution of the number of bottles of liquor and the number of cartons of cigarettes imported by Canadians who have visited the United States for 2 or more days.

a. Find the marginal probability distribution of the number of bottles imported.

P(0 Bottles) =
P(1 Bottle) =

b. Find the marginal probability distribution of the number of cigarette cartons imported.

P(0 Cartons) =
P(1 Carton) =

c. Compute the mean and variance of the number of bottles of liquor imported.

Mean =
Variance =

d. Compute the mean and variance of the number of cigarette cartons imported.

Mean =
Variance =

e. Compute the covariance and the coefficient of correlation.

Covariance =
Coefficient of Correlation =

Seamus asked

by Seamus

4.2k points

1 Answer

Ask a Question

Sabarish · Answer 1 · 2022-06-06T15:23:51+0000

Answer:

(a): Marginal pmf of x

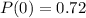
P(0) = 0.72

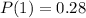
P(1) = 0.28

(b): Marginal pmf of y

P(0) = 0.81

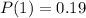
P(1) = 0.19

(c): Mean and Variance of x

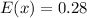
E(x) = 0.28

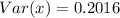
Var(x) = 0.2016

(d): Mean and Variance of y

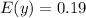
E(y) = 0.19

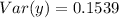
Var(y) = 0.1539

(e): The covariance and the coefficient of correlation

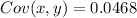
Cov(x,y) = 0.0468

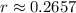
$r \approx 0.2657$

Explanation:

Given

x = bottles

y = carton

See attachment for complete question

Solving (a): Marginal pmf of x

This is calculated as:

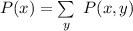
$P(x) = \sum\limits^{}_y\ P(x,y)$

So:

P(0) = P(0,0) + P(0,1)

P(0) = 0.63 + 0.09

P(0) = 0.72

P(1) = P(1,0) + P(1,1)

P(1) = 0.18 + 0.10

P(1) = 0.28

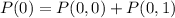
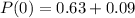
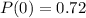
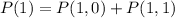
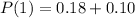
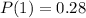
Solving (b): Marginal pmf of y

This is calculated as:

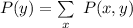
$P(y) = \sum\limits^{}_x\ P(x,y)$

So:

P(0) = P(0,0) + P(1,0)

P(0) = 0.63 + 0.18

P(0) = 0.81

P(1) = P(0,1) + P(1,1)

P(1) = 0.09 + 0.10

P(1) = 0.19

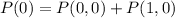
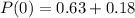
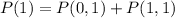
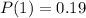
Solving (c): Mean and Variance of x

Mean is calculated as:

$E(x) = \sum( x * P(x))$

So, we have:

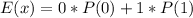
E(x) = 0 * P(0) + 1 * P(1)

E(x) = 0 * 0.72 + 1 * 0.28

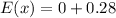
E(x) = 0 + 0.28

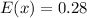
E(x) = 0.28

Variance is calculated as:

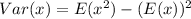
Var(x) = E(x^2) - (E(x))^2

Calculate
E(x^2)

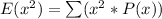
$E(x^2) = \sum( x^2 * P(x))$

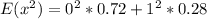
E(x^2) = 0^2 * 0.72 + 1^2 * 0.28

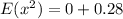
E(x^2) = 0 + 0.28

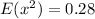
E(x^2) = 0.28

So:

Var(x) = E(x^2) - (E(x))^2

Var(x) = 0.28 - 0.28^2

Var(x) = 0.28 - 0.0784

Var(x) = 0.2016

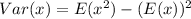
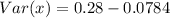
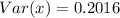
Solving (d): Mean and Variance of y

Mean is calculated as:

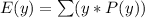
$E(y) = \sum(y * P(y))$

So, we have:

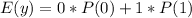
E(y) = 0 * P(0) + 1 * P(1)

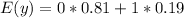
E(y) = 0 * 0.81 + 1 * 0.19

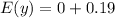
E(y) = 0+0.19

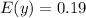
E(y) = 0.19

Variance is calculated as:

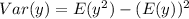
Var(y) = E(y^2) - (E(y))^2

Calculate
E(y^2)

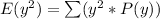
$E(y^2) = \sum(y^2 * P(y))$

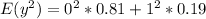
E(y^2) = 0^2 * 0.81 + 1^2 * 0.19

E(y^2) = 0 + 0.19

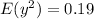
E(y^2) = 0.19

So:

Var(y) = E(y^2) - (E(y))^2

Var(y) = 0.19 - 0.19^2

Var(y) = 0.19 - 0.0361

Var(y) = 0.1539

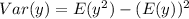
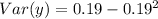
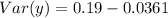
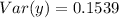
Solving (e): The covariance and the coefficient of correlation

Covariance is calculated as:

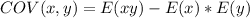
COV(x,y) = E(xy) - E(x) * E(y)

Calculate E(xy)

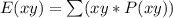
$E(xy) = \sum (xy * P(xy))$

This gives:

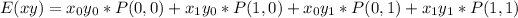
E(xy) = x_0y_0 * P(0,0) + x_1y_0 * P(1,0) +x_0y_1 * P(0,1) + x_1y_1 * P(1,1)

E(xy) = 0*0 * 0.63 + 1*0 * 0.18 +0*1 * 0.09 + 1*1 * 0.1

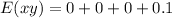
E(xy) = 0+0+0 + 0.1

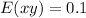
E(xy) = 0.1

So:

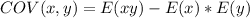
COV(x,y) = E(xy) - E(x) * E(y)

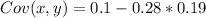
Cov(x,y) = 0.1 - 0.28 * 0.19

Cov(x,y) = 0.1 - 0.0532

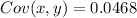
Cov(x,y) = 0.0468

The coefficient of correlation is then calculated as:

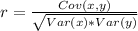
r = (Cov(x,y))/(√(Var(x) * Var(y)))

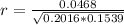
r = (0.0468)/(√(0.2016 * 0.1539))

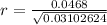
r = (0.0468)/(√(0.03102624))

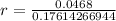
r = (0.0468)/(0.17614266944)

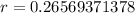
r = 0.26569371378

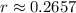$r \approx 0.2657$ --- approximated

Canadians who visit the United States often buy liquor and cigarettes, which are much-example-1

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions