Question

A closed, rigid container holding 0.2 moles of a monatomic ideal gas is placed over a Bunsen burner and heated slowly, starting at a temperature of 300 K. The initial pressure of the ideal gas is atmospheric pressure, and the final pressure is four times the initial pressure.

Determine the following:
a. the change in the internal energy of the gas.
b. the work done by the gas.
c. the heat flow into or out of the gas.

Answer 1

a) 2250 J

b) 0 J

c) 2250 J

Step-by-step explanation:

a) Since, the process is isochoric

the change in internal energy

`\Delta U = n C_v(T_f-T_i)`

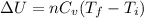
Here, n = 0.2 moles

Cv = 12.5 J/mole.K

We have to find T_f so we can use gas equation as

`(P_1V_1)/(P_2V_2) =(T_i)/(T_f)\\Since, V_1=V_2 [isochoric/process]\\\Rightarrow (P_(atm))/(4P_(atm)) = (300)/(T_f) \\\Rightarrow T_f = 1200 K`

So,
`\Delta U= 0.2*12.5(1200-300)\\=2250 J`

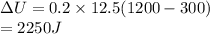
b) Since, the process is isochoric no work shall be done.

c) By first law of thermodynamics we have

`\Delta U = Q-W\\Since, W = 0\\\Delta U = Q\\Therefore, Q = 2250 J`

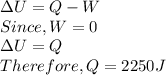
Since, Q is positive 2250 J of heat will flow into the system.