Answer:
a. We fail to reject the null hypothesis
b. p > 0.01
c. The test result is not statistically significant
d. There not is enough statistical evidence to suggest that regular exercise improves academic achievement
Explanation:
No. Physical Exercise (X₂); 3.75, 2.74, 3.42, 1.67, 3, 3.25, 2.65
Physical Exercise (X₁); 4.00, 2.67, 3.65, 2.11, 3.21, 3.60, 2.80
GPAs Pair number; 1, 2, 3, 4, 5, 6, 7
The null hypothesis, H₀; μ₁ ≤ μ₂
The alternative hypothesis, Hₐ; μ₁ > μ₂
From the data, we have;
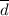 ≈ 0.222857
≈ 0.222857
Where;
d = X₁ - X₂
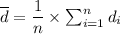
Similarly, we have;
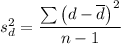
From which we get;
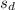 ≈ 0.160905
≈ 0.160905
The critical-t at n - 1 = 7 - 1 = 6 degrees of freedom for α = 1% = 0.01, is given as follows;
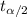 =
=
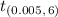 = 3.707
= 3.707
The test statistic, t =
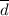 /(
/(
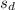 /√n)
/√n)
∴ t = 0.222857/(0.160905/√7) ≈ 3.664
The test statistic , t ≈ 3.664
Therefore, given that the test statistic is smaller than the critical-t,
b. The p-value estimate is p > 0.01
c. The test result is not statistically significant
d. The test result can be reported in a literature as that there is not enough statistical evidence to reject the null hypothesis, therefore, there not is enough statistical evidence to suggest that regular exercise improves academic achievement