Answer:
The calculated value t = 1.3788 < 2.0262 at 0.05 level of significance
the null hypothesis is accepted
There is no significant difference between their counterparts across the nation
Explanation:
Step(i):-
Given that the mean of the U.S residents = 1.65
Given that the size of the sample 'n' = 38
Mean of the sample = 1.84
Given that the standard deviation of the sample (S) = 0.85
Step(ii):-
Null hypothesis:H₀:
There is no significant difference between their counterparts across the nation
Alternative Hypothesis:-H₁:
There is a significant difference between their counterparts across the nation
Test statistic
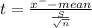
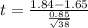
t = 1.3788
Degrees of freedom
ν = n-1 = 38-1 = 37
t₀.₀₅ ,₃₇ = 2.0262
The calculated value t = 1.3788 < 2.0262 at 0.05 level of significance
Null hypothesis is accepted
Final answer:-
There is no significant difference between their counterparts across the nation.