Question

A deli clerk has lunchmeat formed in the shape of a cylinder with a radius of 2 inches and a height of 4 inches. He divides the lunchmeat into two equal sections by making a vertical cut as shown below. What is the shape of the cross section formed by the vertical cut?

Answer 1

The shape of the cross-section is a square

Explanation:

Given

`r =2`

`h = 4`

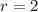
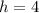
See attachment

Required

The shape of the cross-section

From the attachment, we can see that when the cylinder is cut vertically, the shape formed is a quadrilateral of equal opposite sides.

The dimension of the shape is: the height of the cylinder and the diameter of the base circle

From the given parameters, we have the radius and the height to be:

`r =2`

`h = 4`

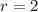
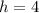
The diameter (d) is:

`d = 2 * r`

`d = 2 * 2`

`d = 4`

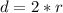
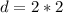
So, the dimension is:

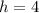`h = 4` and
`d = 4`

Since the height and the diameter have the same lengths, then the shape is a square.