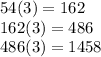Answer:
Common ratio is 3
The three terms are 162, 486, 1458
Explanation:
Given: The first 4 terms of a sequence are
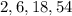
To find:
A. the common ratio
B. the next 3 values in the geometric sequence
Solution:
Geometric sequence is a sequence in which each of the terms is obtained by multiplying the previous term by a fixed number.
A.
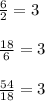
So, the common ratio is

B.
The next three values are as follows: