Question

The two major forces opposing the motion of a vehicle moving on a level road are the rolling resistance of the tires, Fr, and the aerodynamic drag force of the air flowing around the vehicle, Fd, given respectively by Fr, = fW, Fd= CdA1/2 rhoV2 where f and Cd are constants known as the rolling resistance coefficient and drag coefficient, respectively, W and A are the vehicle weight and projected frontal area, respectively, V is the vehicle velocity, and rho is the air density. For a passenger car with W = 3,550 lbf, A = 23.3 ft^2, and Cd = 0.34, and where f = 0.02 and rho = 0.08 lbm/ft^3.

Required:
Determine the power required, in HP, to overcome rolling resistance and aerodynamic drag when V is 55 mph.

Answer 1

The power required to overcome rolling resistance and aerodynamic drag is 19.623 h.p.

Step-by-step explanation:

Let suppose that vehicle is moving at constant velocity. By Newton's Law of Motion, the force given by engine must be equal to the sum of the rolling resistance and the aerodynamic drag force of the air. And by definition of power, we have the following formula:

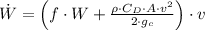`\dot W = \left(f\cdot W +(\rho\cdot C_(D)\cdot A\cdot v^(2))/(2\cdot g_(c)) \right)\cdot v` (1)

Where:

`\dot W`- Power, in pounds-force-feet per second.

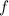`f` - Rolling resistance coefficient, no unit.

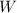`W` - Weight of the passanger car, in pounds-force.

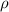`\rho` - Density of air, in pounds-mass per cubic feet.

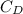`C_(D)` - Drag coefficient, no unit.

`A` - Projected frontal area, in square feet.

`v` - Vehicle speed, in feet per second.

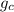`g_(c)` - Pound-mass to pound-force ratio, in pounds-mass to pound-force.

If we know that
`f = 0.02`,
`W = 3,550\,lbf`,
`\rho = 0.08\,(lbm)/(ft^(3))`,
`C_(D) = 0.34`,
`A = 23.3\,ft^(2)`,
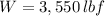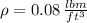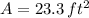`v = 80.685\,(ft)/(s)` and
`g_(c) = 32.174\,(lbm)/(lbf)`, then the power required by the car is:

`\dot W = \left(f\cdot W +(\rho\cdot C_(D)\cdot A\cdot v^(2))/(2\cdot g_(c)) \right)\cdot v`

`\dot W = 10901.941\,(lbf\cdot ft)/(s)`

`\dot W = 19.623\,h.p.`

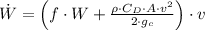
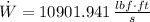
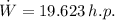
The power required to overcome rolling resistance and aerodynamic drag is 19.623 h.p.