Answer:
L=15
W=21
Step-by-step explanation:
Since it's a frame and the height is not listed, I decided that it was a normal rectangle, instead of a rectangular prism.
In this case, the equation we start with would look something like this:
315 = (17+2x)(11+2x)
2x is necessary because the frame covers the entire shape, meaning that it will apply twice, one for each end.
By simplifying this into standard form, we get:
-4x²-56x+128=0
Next, we plug this equation into the quadratic formula:
x=
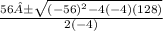 (Please ignore the "A" next to 56, it wont disappear for some reason)
(Please ignore the "A" next to 56, it wont disappear for some reason)
Through simplifying the quadratic formula, we get two answers:
x=-16
x=2
We can't use negatives, so 2 becomes what we use for X.
From here, use the following equations to solve for the corresponding lengths:
L=11+2(2)
W=17+2(2)
Answers:
L=15
W=21
Hope it helped!