Question

Find the slope of the line that passes through each pair of points

A(4, 5) and B(–3, 5)

S(3, –6) and T(3, –9)

Answer 1

A and B: slope = 0

S and T: slope = undefined

Explanation:

To find the slope of the line that passes between a pair of points, use the slope formula,
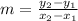`m = (y_2-y_1)/(x_2-x_1)`. Substitute the x and y values of two points into that formula and simplify.

1) Let's try this with the first problem. Substitute the x and y values of (4,5) and (-3,5) into the formula, then solve:

`m = ((5)-(5))/((-3)-(4))\\m = (5-5)/(-3-4) \\m = (0)/(-7) \\m = 0`

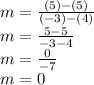
So, the slope of the line between A and B is 0.

2) Do the same with the second problem, substituting the x and y values of (3,-6) and (3,-9):

`m = ((-9)-(-6))/((3)-(3)) \\m = (-9+6)/(3-3) \\m = (-3)/(0) \\`

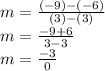
However, we can't divide by zero. So, the slope between points S and T must be undefined.