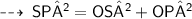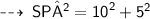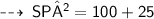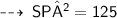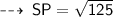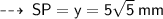Question

Nonsense will be reported!!​

Answer 1

`\qquad \qquad\huge \underline{\boxed{\sf Answer}}`

For the first figure ~

The diagonals of a kite intersect each other at 90°

So, we can apply Pythagoras theorem here :

`\qquad \sf  \dashrightarrow \: CD² = OC² + OD²`

`\qquad \sf  \dashrightarrow \: CD² = {7}^(2) + {9}^(2)`

`\qquad \sf  \dashrightarrow \: CD² = 49 + 81`

`\qquad \sf  \dashrightarrow \: CD² = 130`

`\qquad \sf  \dashrightarrow \: CD=x = √( 130)`

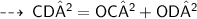
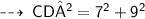
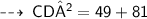
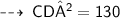
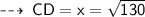
For the second figure ;

we have same concept of kite, and use of Pythagoras theorem !

Also, the diagonal QS bisects diagonal PR

Hence,

`\qquad \sf  \dashrightarrow \: PR = 2 * OR`

`\qquad \sf  \dashrightarrow \: 10 = 2 * OR`

`\qquad \sf  \dashrightarrow \: OR = 10 / 2`

`\qquad \sf  \dashrightarrow \: OR = 5 \: mm`

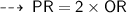
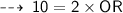
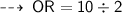
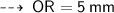
now, apply pythagoras theorem ~

`\qquad \sf  \dashrightarrow \: QR² = OR² + OQ²`

`\qquad \sf  \dashrightarrow \: QR² = {5}^(2) + {6}^(2)`

`\qquad \sf  \dashrightarrow \: QR² = 25 + 36`

`\qquad \sf  \dashrightarrow \: QR² = 61`

`\qquad \sf  \dashrightarrow \: QR=x = √(61) \: mm`

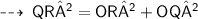
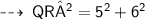
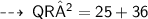
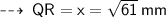
here, 2 OR = 2 OP = PR

so, similarly OP = 5 mm

Applying pythagoras theorem again ;

`\qquad \sf  \dashrightarrow \: SP² = OS² + OP²`

`\qquad \sf  \dashrightarrow \: SP² = {10}^(2) + {5}^(2)`

`\qquad \sf  \dashrightarrow \: SP² = {100}^{} + 25`

`\qquad \sf  \dashrightarrow \: SP² = 125`

`\qquad \sf  \dashrightarrow \: SP = √(125)`

`\qquad \sf  \dashrightarrow \: SP = y = 5√(5) \: mm`