Question

Find the length of the chord made by 3x2 - y2 = 3 and y + x – 5 = 0.

Answer 1

The correct answer is "9√2 units".

Explanation:

The given equations are:

⇒
`3x^2-y^2=3`...(equation 1)

⇒
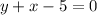`y+x-5=0`...(equation 2)

According to the 2nd equation, we get

⇒
`y+x-5=0`

⇒
`y=5-x`

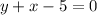
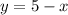
On substituting the value of "y" in the 1st equation, we get

⇒
`3x^2-y^2=3`

`3x^2-(5-x)^2=3`

`3x^2-(25+x^2-10x)=3`

`2x^2+10x-28=0`

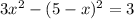
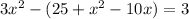
On taking common, we get

`x^2+5x-14=0`

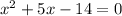
On applying factorization, we get

`x^2+7x-2x-14=0`

`x(x+7)-2(x+7)=0`

`(x+7)(x-2)=0`

`x+7=0`

`x=-7`

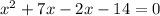
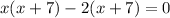
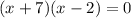
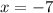
or,

`x-2=0`

`x=2`

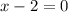
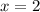
Now,

The points are:

(-7, 12) = (x₁, y₁)

(2, 3) = (x₂, y₂)

By using the distance formula, the length of chord will be:

=
`√((x_2-x_1)^2+(y_2-y_1)^2)`

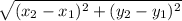
On substituting the values in the above formula, we get

=
`√((2-(-7))^2+(3-12)^2)`

=
`√((9)^2+(-9)^2)`

=
`√(81+81)`

=
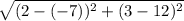
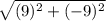
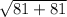
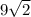`9 √(2)` units