Question

The length of a rectangle is 3 cm less than its width what are the dimensions of the rectangle if its area is 270 cm²

Answer 1

Given:

The length of a rectangle is 3 cm less than its width.

The area of the rectangle is 270 cm².

To find:

The dimensions of the rectangle.

Solution:

Let x be the width of the rectangle. Then,

`\text{Length}=x-3`

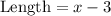
Area of a rectangle is:

`\text{Area}=\text{Length}* \text{width}`

`270=(x-3)(x)`

`270=x^2-3x`

`0=x^2-3x-270`

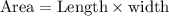
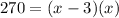
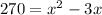
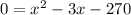
Splitting the middle term, we get

`x^2-18x+15x-270=0`

`x(x-18)+15(x-18)=0`

`(x-18)(x+15)=0`

`x=18,-15`

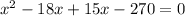
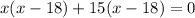
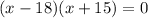
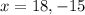
Width of the rectangle cannot be negative. So, the only value of x is 18.

`Width=18`

`Length=18-3`

`Length=15`

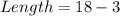
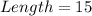
Therefore, the length of the rectangle is 15 cm and the width of the rectangle is 18 cm.