Question

Can you please help? The question is in the picture picture. thank you

Answer 1

Given:

The value is
`(√(2))/(2)`.

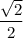To find:

The values from the given options which are equal to the given value.

Solution:

We have,

`(√(2))/(2)`

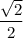
It can be written as:

`(√(2))/(2)=(1)/(√(2))`

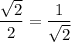
From the standard trigonometric table, we get

`\sin 30^\circ=(1)/(2)`

`\sin 45^\circ=(1)/(√(2))`

`\cos 45^\circ=(1)/(√(2))`

`\cos 60^\circ=(1)/(2)`

`\tan 30^\circ=(1)/(√(3))`

`\tan 45^\circ=1`

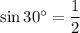
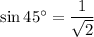
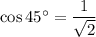
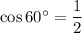
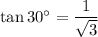
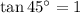
From the above values it is clear that the value of
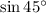`\sin 45^\circ` and
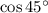`\cos 45^\circ` are equal to
`(1)/(√(2))`.

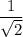Therefore,
`\sin 45^\circ` and
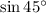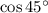`\cos 45^\circ` and equal to
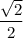`(√(2))/(2)`. So, options B and C are correct.