Hello!
This is a question relating a quadratic equation to the vertex and roots.
Since this parabola has a negative a value, the vertex will be the maximum height that this rocket reaches.
We can find the vertex (h,k) with the following equations.

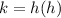

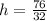
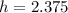
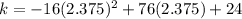
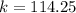
We can interpret the values like this:
At
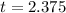 seconds after the rocket was launched, the rocket reached its maximum height of
seconds after the rocket was launched, the rocket reached its maximum height of
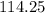 feet.
feet.
Since the y-intercept is at
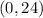 and this is a negative parabola, there will only be one positive root, which will be how long our rocket is in the air.
and this is a negative parabola, there will only be one positive root, which will be how long our rocket is in the air.
Use the quadratic formula.
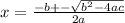
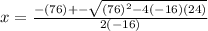
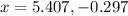
Since we are searching for our positive root, this rocket is in the air for 5.407 seconds.
Hope this helps!