Answer:

Explanation:
In order to solve this we can start by drawing a sketch of the problem (see attached picture)
So fist, let's take the general form of a sinusoidal movement:
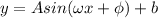
where:
A= amplitude
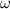 = angular frequency
= angular frequency
x= time
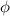 = horizontal shift
= horizontal shift
b= vertical shift.
In this case, the amplitude will be the maximum distance between the center of the wheel and the highest or lowest point of the trajectory, in this case:
A= 13in - 0.5in =12.5 in
The angular frequency is how many radians the wheel will turn in a minute, so we get:
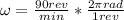
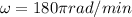
Generally, the sin function will start at the center of the circular movement. In this case, since it starts on the lowest point, we can say that the graph moves right by
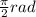 , so in this case:
, so in this case:

and finally, the vertical shift is the distance between the center of the circular movement and the ground so in this case:
b=13in
so when putting it all together we get our equation to be:
