Answer:
The test statistic is t = 3.24.
Explanation:
We want to test the hypothesis that the fuel additive has mean mpg less than the mean mpg without the additive.
This means that the null hypothesis is that the difference is less than 0, while the alternate hypothesis is that the difference is 0 or more.
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation of the sample and n is the size of the sample.
is the standard deviation of the sample and n is the size of the sample.
0 is tested at the null hypothesis:
This means that
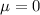
Randomly select 10 cars
This means that

The sample mean difference in gas mileage (mpg with additive - mpg without additive) is 0.41 mpg with a sample variance of 0.16.
This means that
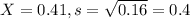
Calculate the test statistic.

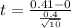
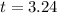
The test statistic is t = 3.24.