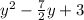Question

If m and n are the zeroes of the polynomial 6y 2 -7y – 2, find a polynomial whose zeroes are 1/m and 1/n

Answer 1

`y^2-(7)/(2)y+3`

Explanation:

Given polynomial is,

6y² - 7y - 2

Fro the zeros of the given polynomial,

6y² - 7y - 2 = 0

6y² - 4y - 3y - 2 = 0

2y(3y - 2) - 1(3y - 2) = 0

(2y - 1)(3y - 2) = 0

(2y - 1) = 0

y =
`(1)/(2)`

(3y - 2) = 0

y =
`(2)/(3)`

Therefore, zeros of this polynomial are m =
`(1)/(2)` and n =
`(2)/(3)`

If a polynomial has zeros as
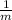`(1)/(m)` and
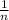`(1)/(n)` then the zeros will be
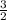`(3)/(2)` and 2.

Polynomial will be,

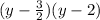
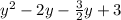
`(y-(3)/(2))(y-2)`

=
`y(y-2)-(3)/(2)(y-2)`

=
`y^2-2y-(3)/(2)y+3`

=
`y^2-(7)/(2)y+3`