Answer:
There are 504 different codes.
Explanation:
First some definitions:
If we have a set of N elements and we want to make combinations of K of these elements, the total number of different combinations is:
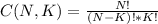
And in the case of codes we need to also take in account the permutations of the elements (because is not the same DAC as CDA)
For a set of K different elements, the number of permutations is K!
We can not duplicate letters, then the first thing we need to do is to count the al the unique letters that appear in the word duplicate, these are:
{D, U, P, L, I, C, A, T, E}
We have a total of 9 letters, and the code must have 3, then:
N = 9
K = 3
The total number of different combinations is:
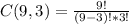
And each one of these combinations needs to be multiplied for the different permutations, then the total number of different codes is:
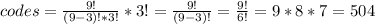
There are 504 different codes.