Question

Solve the quadratic equation by factoring.

4x² - 20x + 28 = 3

A) x = 5
B) x = 5/2
C) x = 2/5
D) x = - 5/2

Answer 1

B) x = 5/2

Explanation:

4x² - 20x + 28 = 3

Move terms to the left side

4x² - 20x + 28 - 3 = 0

Subtract the numbers

4x² - 20x + 25 = 0

Use the quadratic formula

`x =\frac{-b+\sqrt{b^(2)-4ac } }{2a}`

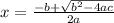
Once in standard form, identify a, b, and c from the original equation and plug them into the quadratic formula.

4x² - 20x + 25 = 0

a = 4

b = -20

c = 25

x =
`\frac{-(-20)+\sqrt{(-20)^(2)-4x4x25 } }{2x4}`

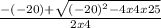
Evaluate the exponent

x =
`(20+√(400-4x4x25 ) )/(2x4)`

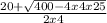
Multiply the numbers

x =
`(20+√(400-400 ) )/(2x4)`

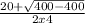
Subtract the numbers

x =
`(20+√(0) )/(2x4)`

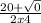
Evaluate the square root

x =
`(20+0 )/(2x4)`

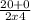
Add zero

x = 20 / 2 x 4

Multiply the numbers

x = 20 / 8

Cancel terms that are in both the numerator and denominator

x = 5/2

Answer 2

B) x = 5/2

Explanation:

subtract 3 from each side to get:

4x² - 20x + 25 = 0

this is the difference of 2 squares:

(2x -5)² = 0

one solution, x = 5/2