Question

Tomas learned that the product of the polynomials
`(a+b)(a^2-ab+b^2)` was a special pattern that would result in a sum of cubes,
`a^3+b^3`.

His teacher put four products on the board and asked the class to identify which product would result in a sum of cubes if
`a=2x` and
`b=y`.

Answer 1

We are provided , Tomas learned that a³ + b³ = (a + b ) ( a² - ab + b² ) , and his teacher writes four products on the board and we have to tell that which product suits the best if a = 2x and b = y

Now , putting a = 2x , b = y in the given formula we have :

`{:\implies \quad \sf (2x)^(3)+(y)^(3)=(2x+y)\{(2x)^(2)-2\cdot x\cdot y+(y)^(2)\}}`

`{:\implies \quad \bf \therefore \quad \underline{\underline{(2x)^(3)+(y)^(3)=(2x+y)(4x^(2)-2xy+y^(2))}}}`

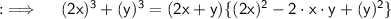
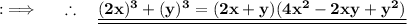
Hence , The product (2x+y) (4x²-2xy+y²) would result in the sum of cubes of 2x & y :D