Question

A machine, when working properly, produces 5% or less defective items. Whenever the machine produces significantly greater than 5% defective items, it needs repair. A random sample of 300 items taken from the production line contained 27 defective items. Test at the 1% significance level if the percentage of defective items produced by this machine is greater than 5%.

Answer 1

The pvalue of the test is 0.0007 < 0.01, which means that we reject the null hypothesis and accept the alternate hypothesis that the percentage of defective items produced by this machine is greater than 5%.

Explanation:

A machine, when working properly, produces 5% or less defective items.

This means that the null hypothesis is:

`H_0: p \leq 0.05`

Test if the percentage of defective items produced by this machine is greater than 5%.

This means that the alternate hypothesis is:

`H_a: p > 0.05`

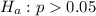
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

0.05 is tested at the null hypothesis:

This means that
`\mu = 0.05, \sigma = √(0.05*0.95)`

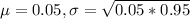
A random sample of 300 items taken from the production line contained 27 defective items.

This means that
`n = 300, X = (27)/(300) = 0.09`

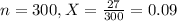
Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.09 - 0.05)/((√(0.05*0.95))/(√(300)))`

`z = 3.18`

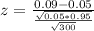
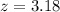
Pvalue of the test:

Testing if the mean is greater than a value, which means that the pvalue of the test is 1 subtracted by the pvalue of Z = 3.18, which is the probability of a finding a sample proportion of 0.09 or higher.

Looking at the Z-table, Z = 3.18 has a pvalue of 0.9993

1 - 0.9993 = 0.0007

The pvalue of the test is 0.0007 < 0.01, which means that we reject the null hypothesis and accept the alternate hypothesis that the percentage of defective items produced by this machine is greater than 5%.