Question

The specification for the pull strength of a wire that connects an integrated circuit to its frame is 10 g or more. In a sample of 86 units made with gold wire, 68 met the specification, and in a sample of 120 units made with aluminum wire, 105 met the specification. Let pX represent the population proportion units made with gold wire that meet the specification and let pY represent the population proportion units made with aluminum wire that meet the specification. Find a 95% confidence interval for the difference

Answer 1

The 95% confidence interval for the difference is (-0.1888, 0.0202).

Explanation:

Difference between proportions:

The distribution of the difference between two proportions has mean of the difference between these proportions and standard deviation is the square root of the sum of the variances. So

In a sample of 86 units made with gold wire, 68 met the specification

This means that:

`pX = (68)/(86) = 0.7907`

`sX = \sqrt{(0.7907*0.2093)/(86)} = 0.0439`

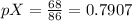
In a sample of 120 units made with aluminum wire, 105 met the specification.

This means that:

`pY = (105)/(120) = 0.875`

`sY = \sqrt{(0.875*0.125)/(120)} = 0.0302`

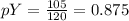
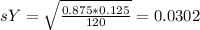
Difference:

`p = pX - pY = 0.7907 - 0.875 = -0.0843`

`s = √(sX^2 + sY^2) = √(0.0439^2+0.0302^2) = 0.0533`

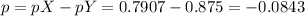
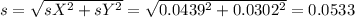
Confidence interval:

`p \pm zs`

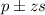
In which z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`, with
`\alpha` being 1 subtracted by the confidence level.

95% confidence level

So
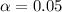`\alpha = 0.05`, z is the value of Z that has a pvalue of
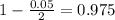`1 - (0.05)/(2) = 0.975`, so
`Z = 1.96`.

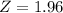Lower bound of the interval:

`p - zs = -0.0843 - 1.96*0.0533 = -0.1888`

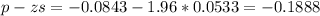
Upper bound of the interval:

`p + zs = -0.0843 + 1.96*0.0533 = 0.0202`

The 95% confidence interval for the difference is (-0.1888, 0.0202).