Question

The pulse rates of 174 randomly selected adult males vary from a low of 39 bpm to a high of 111 bpm. Find the minimum sample size required to estimate the mean pulse rate of adult males. Assume that we want 90% confidence that the sample mean is within 3 bpm of the population mean. Complete parts​ (a) through​ (c) below. a. Find the sample size using the range rule of thumb to estimate σ.

Answer 1

a. The sample size is approximately 97 adults

Explanation:

The given parameters are;

The number of adults surveyed, n = 174

The lowest value of the pulse rate = 39 bpm

The highest value of the pulse rate = 111 bpm

The level of confidence used for determining the sample size = 90%

The given sample mean = 3 pm of the population mean

a. The range rule of thumb states that the standard deviation is approximately one quarter (1/4) of the range

The range = 111 bpm - 39 bpm = 72 bpm

Therefore, the standard deviation, σ = 72 bpm/4 = 18 bpm

The sample size, 'N', is given as follows;

`N = (z^2 \cdot p \cdot q)/(e^2)`

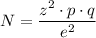
Where;

N = The sample size

z = The confidence level, 90% (z-score at 90% = 1.645)

p·q = σ² = 18² = 324

e² = 3² = 9

`N = (1.645^2 * 324)/(3^2) = 97.4169`

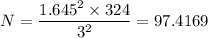
Therefore the appropriate sample size, N ≈ 97 adults.