Answer:
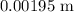

Step-by-step explanation:
m = Order = 1
D = Distance between screen and slit = 3.09 m
d = Slit distance = 1.01 mm
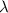 = Wavelength = 639 nm
= Wavelength = 639 nm
Distance from the first bright fringe from the central bright fringe is given by
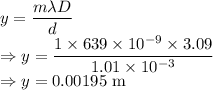
Distance from the first bright fringe from the central bright fringe is
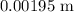
Distance from the second dark fringe from the central bright fringe is given by
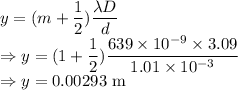
Distance from the second dark fringe from the central bright fringe is
 .
.