Answer:
See below.
Explanation:
For an equation like
 to have no solution, the equation has to be false.
to have no solution, the equation has to be false.
To make an equation false, we let a = c. That’d make a and c have same value, when we transport cr to subtract ar, we’ll get 0.
So if a = c, the equation is
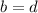 now that we have b = d. The equation has to be false to have no solutions, hence b and d must not equal to one another.
now that we have b = d. The equation has to be false to have no solutions, hence b and d must not equal to one another.
Summary
- When a = c, the new equation is b = d as ar and cr having same value, when subtracted, the remain is 0+b=d.
- b = d means that the value of b and d are equal but that makes the solutions to be infinitely many. Therefore, we cannot let b = d.
- From second, b ≠ d.
- a = c but b ≠ d
Let me know if you have any questions regarding this question or for clarification.