Question

Researchers investigated whether providing a fancy, foil-wrapped piece of chocolate with the dinner bill would lead to higher tips than not providing such a treat. Sixty-four dinner parties at a restaurant in Ithaca, NY were randomly assigned to receive such a piece of chocolate or not with their dinner bill. Of the 32 parties who received the chocolate, the average tip (as a percentage of the bill) was 17.84%, with a standard deviation of 3.06%. Of the 32 parties who did not receive the chocolate, the average tip (as a percentage of the bill) was 15.06%, with a standard deviation of 1.89%. Determine a 96% confidence interval for the size of the difference in average tips between the two groups

Answer 1

The 96% confidence interval for the size of the difference in average tips between the two groups is (1.47%, 4.09%).

Explanation:

Before building the confidence interval, we need to understand the central limit theorem and subtraction of normal variables.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

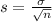For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

Subtraction of normal variables:

When we subtract normal variables, the mean is the subtraction of the means while the standard deciation is the square root of the sum of the variances.

Of the 32 parties who received the chocolate, the average tip (as a percentage of the bill) was 17.84%, with a standard deviation of 3.06%.

This means that:

`\mu_(C) = 17.84, s_(C) = (3.06)/(√(32)) = 0.541`

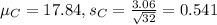
Of the 32 parties who did not receive the chocolate, the average tip (as a percentage of the bill) was 15.06%, with a standard deviation of 1.89%.

This means that:

`\mu_(NC) = 15.06, s_(NC) = (1.89)/(√(32)) = 0.3341`

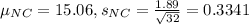
Difference in average tips

The distribution has mean:

`\mu = \mu_(C) - \mu_(NC) = 17.84 - 15.06 = 2.78`

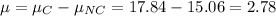
Standard deviation:

`s = \sqrt{s_(C)^2 + s_(NC)^2} = √(0.541^2 + 0.3341^2) = 0.6358`

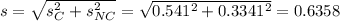
96% confidence interval

We have that to find our
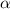`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1 - 0.96)/(2) = 0.02`

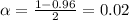
Now, we have to find z in the Ztable as such z has a pvalue of
`1 - \alpha`.

That is z with a pvalue of
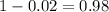`1 - 0.02 = 0.98`, so Z = 2.054.

Now, find the margin of error M as such

`M = zs`

`M = 2.054*0.6358 = 1.31`

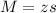
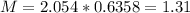
The lower end of the interval is the sample mean subtracted by M. So it is 2.78% - 1.31% = 1.47%

The upper end of the interval is the sample mean added to M. So it is 2.78% + 1.31% = 4.09%

The 96% confidence interval for the size of the difference in average tips between the two groups is (1.47%, 4.09%).