Question

A refrigerator is 1.8m tall, lm wide,and 0.8m deep.The center of mass is lm from the bottom, 0.5m from the side, and 0.6m from the front. it weighs 1300N. When pushing it back into its position in the kitchen, you must push on the front side. If you push horizontally from a height of 1.5m above the bottom, what is the maximum pushing force you can exert to avoid tipping the refrigerator

Answer 1

F = 520 N

Step-by-step explanation:

For this exercise the rotational equilibrium equation should be used

Σ τ = 0

Let's set a reference system with the origin at the back of the refrigerator and the counterclockwise rotation as positive. On the x-axis it is horizontal directed outward, eg the horizontal y-axis directed to the side and the z-axis vertical

Torque is

τ = F x r

the bold indicate vectors, we analyze each force

the applied force is horizontal along the -x axis, the arm (perpendicular distance) is directed in the z axis,

The weight of the body is the vertical direction of the z-axis, so the arm is on the x-axis

-F z + W x = 0

F z = W x

F =
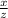`(x)/(z)` W

The exercise indicates the point of application of the force z = 1.5 m and the weight is placed in the center of mass of the body x = 0.6 m, we are assuming that the force is applied in the wide center of the refrigerator

let's calculate

F = 1300 0.6 / 1.5

F = 520 N