Answer:
95% confidence interval for the proportion of smokers who have tried to quit within the past year
(0.47956 ,0.50620)
Explanation:
Step(i):-
Given that National Center for Health Statistics interviewed 5409 adult smokers in 2015
Sample size 'n' = 5409
Given that 2666 of them said they had tried to quit smoking during the past year.
proportion
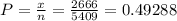
Q = 1 - P = 1 - 0.49288 = 0.50712
Step(ii):-
95% confidence interval for the proportion of smokers who have tried to quit within the past year
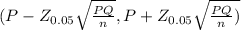
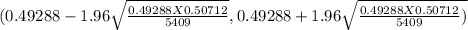
(0.49288 - 0.01332 , 0.49288+0.01332)
(0.47956 , 0.50620 )
Final answer:-
95% confidence interval for the proportion of smokers who have tried to quit within the past year
(0.47956 ,0.50620)