Question

Very large forces are produced in joints when a person jumps from some height to the ground. (a) Calculate the magnitude of the force (in N) produced if a 62.0 kg person jumps from a 0.800 m-high ledge and lands stiffly, compressing joint material 1.50 cm as a result. (Be certain to include the weight of the person.) N (b) In practice the knees bend almost involuntarily to help extend the distance over which you stop. Calculate the magnitude of the force (in N) produced if the stopping distance is 0.300 m. N (c) Compare both forces with the weight of the person.

Answer 1

a) F = 3.3 10⁴ N, b) F = 2.2 10³ N, c) force when rigid is 15 times greater than when bending the knees

Step-by-step explanation:

For this exercise we can use the relationship between work and the variation of kinetic energy

K₀ = ½ m v²

the final kinetic energy is zero because the person is stationary

W = (∑ F) x

W = W x - F w

the weight is in the same direction of the displacement therefore the work is positive and the force applied, by the floor, is in the opposite direction to the displacement, consequently the work is negative

we substitute

( W- F ) x = 0-K₀

F = W + K₀ /x

F = mg +
`(1)/(2) (mv^2 )/(2x)`

F = m ( g+
`(v^2 )/(2x )` )

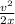Let's use kinematics to find the velocity of the person when reaching the floor

v² = v₀² - 2g (y + y₀)

the initial velocity is true and when reaching the ground y = 0

v² = -2 g (0-yo)

we calculate

v =
`√(2 ] 9.8 \ 0.800)`

v = - 3.96 m/s

the direction of this velocity is vertical down

let's calculate

a) x = 1.50 cm = 0.0150 m

F = 62.0 (3.96² / 2 0.0150 + 9.8)

F = 3.3 10⁴ N

b) x = 30 cm = 0.30 m

F = 62.0 (3.96² / 2 0.30 + 9.8)

F = 2.2 10³ N

c) to compare the force let's look for the relationship between the two

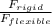`(F_(rigid) )/( F_(flexible) )` = 3.3 10⁴ / 2.2 10³

\frac{F_{rigid} }{ F_{flexible} } = 15

therefore see that the force when rigid is 15 times greater than when bending the knees