Question

A red die and a blue die are rolled. You win or lose money depending on the sum of the values of the two dice. If the sum is 6 or 10, you win $4. If the sum is 5, 9, or 12, you win $1. If the sum is any other value (2, 3, 4, 7, 8, or 11), you lose $2. Let X be a random variable that corresponds to your net winnings in dollars. What is the expected value of X

Answer 1

The expected value of X is $0.0833.

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

For each dice, there are 6 possible outcomes(values from 1 to 6). So for 2 dices, there are
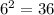`6^2 = 36` desired outcomes.

Desired outcomes:

Sum 5: (1,4), (2,3), (3,2), (4,1).

Sum 6: (1,5),(2,4),(3,3),(4,2),(5,1)

Sum of 9: (3,6), (4,5), (5,4), (6,3)

Sum of 10: (4,6), (5,5), (6,4)

Sum of 12: (6,6)

Probabilities:

5 + 3 = 8 outcomes in which the sum is 6 or 10, that is, 8/36 probability of winning $4.

4 + 4 + 1 = 9 outcomes in which the 5, 9, or 12, that is, 9/36 probability of winning $1.

36 - (8 + 9) = 36 - 17 = 19 remaining outcomes, that is, 19/36 probability of losing $2.

What is the expected value of X?

Multiplication of each outcome by its probability. So

`E(X) = (8)/(36)*4 + (9)/(36)*1 - (19)/(36)*2 = (8*4 + 9*1 - 19*2)/(36) = (32 + 9 - 38)/(36) = (3)/(36) = 0.0833`

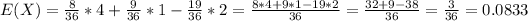
The expected value of X is $0.0833.