Answer:
1.27
Explanation:
When completing word problems, it's always important to first turn everything into an equation.
The volume of a rectangular box is:
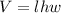
Where l is the length, h is the height, and w is the width.
Which we can write down the equation:
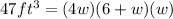
Next up, distribute:
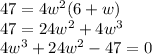
We have a cubic equation, you can solve it using a calculator.
We have three solutions, and they are:
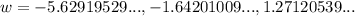
Since lengths cannot be negative, there is just one solution:
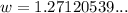
And rounding it gives:
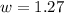
And don't forget to put ft at the end!