Answer:
he sphere that uses less time is sphere A
Step-by-step explanation:
Let's start with ball A, for this let's use the kinematics relations
v² = v₀² - 2g (y-y₀)
indicate that the sphere is released therefore its initial velocity is zero and when it reaches the floor its height is zero y = 0
v² = 0 - 2 g (0- y₀)
v =
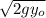
v =
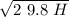
v = 4.427 √H
Now let's work the sphere B, in this case it rolls down a ramp, let's use the conservation of energy
starting point. At the highest point, before you start to move
Em₀ = U = m g y
final point. At the bottom of the ramp
Em_f = K = ½ m v² + ½ I w²
notice that we include the kinetic energy of translation and rotation
energy is conserved
Em₀ = Em_f
mg H = ½ m v² + ½ I w²
angular and linear velocity are related
v = w r
w = v / r
the momentorot of inertia indicates that it is worth
I =
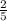 m r²
m r²
we substitute
m g H = ½ m v² + ½ (
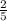 m r²) (
m r²) (
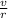 )²
)²
gH =
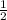 v² +
v² +
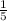 v² =
v² =
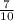 v²
v²
v =
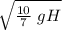
v =
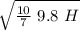
v=3.742 √H
Taking the final speeds of the sphere, let's analyze the distance traveled, sphere A falls into the air, so the distance traveled is H. The ball B rolls in a plane, so the distance (L) traveled can be found with trigonometry
sin θ = H / L
L = H /sin θ
we can see that L> H
In summary, ball A arrives with more speed and travels a shorter distance, therefore it must use a shorter time
Consequently the sphere that uses less time is sphere A